In continuation of the investigation we had in class this week, I've decided try to come up with a solution to find the maximum product of any given integer.
I have discovered that for any integer larger than 3, it can always be written as a combination of 2's and 3's, and for any integer larger than 4 (at 4, the max product is 4 itself), the product of a combination of these 2's and 2's is always going to be bigger than itself.
But how do you make sure that it's the largest possible product? We need the product to be the largest combination of 3's that can be made from this number. In doing so, we break it down to 2 cases:
Multiple of 3: then the product will always be 3^(multiples of 3 in number).
Else: no matter if it's an odd or even number, we need to break this number down until we find a combination of 3's. And since we know that this product is ONLY composed of 2's and 3's, the best way to do this would be to remove a 2 from this number, and try to make the rest divisible by 3.
At this point, my logic is starting to piece together into a function!
So consider the following recursive implementation of max_product:
def max_product(num):
if num == 1:
return 1
elif num == 2:
return 2
elif num % 3 == 0:
return 3 ** (num // 3)
else:
return 2 * max_product(num - 2)
The function will recursively combine the largest possible number of 3's with 2's to create the largest product,
so we can let the function do the rest of the work, and we're done!
Good luck to everyone on the exam! I'm really glad I have a whole week after my calculus exam to sort through everything we learned this semester.
*'``・*。
| `*。
,。∩ *
+ (´∀` ) *。+゜
`*。 ヽ、 つ *゜*
`・+。*・'⊃+゜
☆ ∪~。*゜
`・+。*・
Catherine's CSC165 Adventures
Catherine's captain's log for CSC165 Winter 2013
Friday 5 April 2013
Wednesday 3 April 2013
After Assignment 3
After finishing assignment 3, I feel like I definitely have a better understanding of big O and big Omega, and I'm definitely now capable to deal with questions like this on the exam (although I will definitely be doing more practice on this before the exam anyway).
I found the idea of big Theta very interesting, especially since on the assignment, my answers for question 1 & 2 can be combined to form a big Theta proof. The idea that a function can be both bounded above AND below by a single function (multiplied by different constants) is very fascinating to me, and this is definitely something that is going to be useful in the future for calculating efficiency, especially because we're already beginning to see implementation of big O and big Omega in calculating the efficiency of our functions in CSC148, and understanding of this concept definitely gave everyone in out class a head start compared to people who didn't take this course.
The use of limits in proving big O and big Omega was confusing at first, but then I realized that it was just the observation of the end behaviour relationship between the two functions. For big Omega, if the limit f(x) /g(x) approaches a real number L, then that means g(x) will at one point grow much faster than f(x), so f(x) can no longer be bounded below by g(x). Otherwise, if the limit of f(x) /g(x) approaches infinity, then that means f(x) will continue to grow much faster than g(x), so g(x) is always a lower bound for f(x). I used a similar logic to prove using limits for big O as well.
I really hope that my understanding of this material is correct, I guess I'll double check while I'm studying for the exam!
∧_∧
ry´・ω・`ヽっ
`! i
ゝc_c_,.ノ
(
)
.∧_∧.(
(´・ω・ ∩
o ,ノ
O_ .ノ
.(ノ
━━
Saturday 30 March 2013
Non-computable vs computable functions
So I am currently working on assignment 3, and was able to draft out my proofs for question 1 - 4 pretty easily, but I found myself stuck for the longest time on coming up with a proof for question 5.
And through reviewing the course notes and lecture slides, I was able to find a clue:
Clue 1. If f reduces to g, then f can be implemented using g and perhaps some other functions, like how halt(f, i) can be created using initialized(g, v) and f_prime(x).
So I began by trying to re-create halt with the implementation of true_that, which I was able to do with the help of another function. But yet, for the longest time, I still couldn't link this piece with an idea for a conclusive solution. And then I realized (because I'm really slow otherwise this shouldn't have taken a whole day):
Clue 2. Then if f is non-computable, then that means g is also non-computable. (Like halt, which we've already proven in class to be non-computable -and we already know what f ang g are in this case, hint hint).
It took me an entire day from when I first started working on the assignment to reach this epiphany, so I decided to take the time and share it with the world (obviously I can't say exactly HOW I did it, but this should definitely set whoever just happens to be desperately looking for help on the right track. And if you're desperate enough to feel the need to browse through 150 slogs, then props to you, and you're welcome (hopefully).)
Now I'm going to go back to pasting all my notations back onto MS word clipboard, so I can write my proofs properly. Why can't I just save them permanently, ugh.
I guess I'm just having a harder time than I thought grasping the idea of a well-defined, yet non-computable function, because it's so abstract and very difficult to visualize. But I do find the idea of an almost paradoxical function fascinating, and will probably review this topic in finer detail for the exam.
Good luck to everyone, hope you'll have an easier time than I do with the last one.
Δ~~~~Δ
ξ ・ェ・ ξ ξ ~ ξ ξ ξ ξ “~~~~〇 ξ ξ ξ ξ ξ~~~ξ ξ ξ_ξξ_ξ ξ_ξξ_ξ ヽ(´・ω・)ノ | / UU"
P.S: I follow this japanese emoji twitter, so if you think I'm ever going to run out of these, you are wrong.
And through reviewing the course notes and lecture slides, I was able to find a clue:
Clue 1. If f reduces to g, then f can be implemented using g and perhaps some other functions, like how halt(f, i) can be created using initialized(g, v) and f_prime(x).
So I began by trying to re-create halt with the implementation of true_that, which I was able to do with the help of another function. But yet, for the longest time, I still couldn't link this piece with an idea for a conclusive solution. And then I realized (because I'm really slow otherwise this shouldn't have taken a whole day):
Clue 2. Then if f is non-computable, then that means g is also non-computable. (Like halt, which we've already proven in class to be non-computable -and we already know what f ang g are in this case, hint hint).
It took me an entire day from when I first started working on the assignment to reach this epiphany, so I decided to take the time and share it with the world (obviously I can't say exactly HOW I did it, but this should definitely set whoever just happens to be desperately looking for help on the right track. And if you're desperate enough to feel the need to browse through 150 slogs, then props to you, and you're welcome (hopefully).)
Now I'm going to go back to pasting all my notations back onto MS word clipboard, so I can write my proofs properly. Why can't I just save them permanently, ugh.
I guess I'm just having a harder time than I thought grasping the idea of a well-defined, yet non-computable function, because it's so abstract and very difficult to visualize. But I do find the idea of an almost paradoxical function fascinating, and will probably review this topic in finer detail for the exam.
Good luck to everyone, hope you'll have an easier time than I do with the last one.
Δ~~~~Δ
ξ ・ェ・ ξ ξ ~ ξ ξ ξ ξ “~~~~〇 ξ ξ ξ ξ ξ~~~ξ ξ ξ_ξξ_ξ ξ_ξξ_ξ ヽ(´・ω・)ノ | / UU"
P.S: I follow this japanese emoji twitter, so if you think I'm ever going to run out of these, you are wrong.
Saturday 23 March 2013
Thoughts about the current material
Since this week has been a little more hectic than I thought, I probably won't be able to tackle the problem-solving tasks alongside with assignment 3 until the long weekend.
I'm starting to get the grasp on 'Big O' and 'Big Omega' in terms of bounding the limit behaviour of a certain function using another function. This is definitely an interesting concept, and will probably be very useful in further courses, as I have found a lot of the other material in the course to be useful in proofs for other courses as well (I have pretty much substituted all 'for all' and there exists' with notation in my notes for other classes too, go figure). Even after the tutorial last week, I'm still having a bit of trouble understanding how to do proofs for 'Big O' and 'Big Omega', but I guess doing the assignment will certainly give me enough practice in preparation for the final exam. (There's only a little more than a month to go, this semester flew by so fast!)
I'm starting to get the grasp on 'Big O' and 'Big Omega' in terms of bounding the limit behaviour of a certain function using another function. This is definitely an interesting concept, and will probably be very useful in further courses, as I have found a lot of the other material in the course to be useful in proofs for other courses as well (I have pretty much substituted all 'for all' and there exists' with notation in my notes for other classes too, go figure). Even after the tutorial last week, I'm still having a bit of trouble understanding how to do proofs for 'Big O' and 'Big Omega', but I guess doing the assignment will certainly give me enough practice in preparation for the final exam. (There's only a little more than a month to go, this semester flew by so fast!)
⊹⋛⋋( ՞ਊ ՞)⋌⋚⊹
Saturday 16 March 2013
Catherine_sucks_at_keeping_promises.jpg
I know it's already technically Sunday so a post is kinda overdue (but I posted on Thursday so that kind of counts, right?).
I'm currently trying to figure out the solution to the penny pile problem, there are some solutions up on the website but I don't want any spoilers! Hopefully I'll have a full solution up by Monday night, but my weekend seems pretty packed at the moment, since I have 2 pretty difficult tests next week.
Anyway, I'm gonna try my best to figure this out and post my solution on Monday (if not, it's probably gonna be Thursday again), and then probably start reviewing some of the algorithms, which I haven't really had a chance to do, given the sheer volume of work that I'm currently buried under.
I'm currently trying to figure out the solution to the penny pile problem, there are some solutions up on the website but I don't want any spoilers! Hopefully I'll have a full solution up by Monday night, but my weekend seems pretty packed at the moment, since I have 2 pretty difficult tests next week.
Anyway, I'm gonna try my best to figure this out and post my solution on Monday (if not, it's probably gonna be Thursday again), and then probably start reviewing some of the algorithms, which I haven't really had a chance to do, given the sheer volume of work that I'm currently buried under.
.・゜゜・(/。\)・゜゜・.
Thursday 14 March 2013
Studying for Test 2
Since test 2 is tomorrow, I will be spending the night reviewing the material that we need to know (aka proofing), and piecing together a 'cheat sheet' that will (hopefully) help me during the test just in case I somehow blank out and forget natural and real numbers are (sure, laugh at me now, but things like this are more likely to happen than you's think).
I feel that through the large amount proofing we had to do in assignment 2, I've got a pretty solid fundamental understanding of the structuring and execution of a good proof, although delta epsilons have been haunting me since the day we introduced it in calculus, so I'll definitely be paying very close attention to those.
Some other helpful things I decided to include:
Ceiling(x): the smallest integer no smaller than x
Prove ]x[ + 1 > x:
Since ]x[ + 1 > ]x[ and we know ]x[ > x (by definition of ceiling)
Then ]x[ + 1 > ]x[ >= x
So ]x[ + 1 > x
Strategies for proofs:
1. Sometimes changing the direction and proving the contrapositive is easier.
Example: For all whole numbers x, if x^ 2 , then x is even.
Proving directly would be difficult, but proving that if x is not even, then x^2 is not even
is fairly simple to do.
2. Disprove a statement by negation (I find it simpler and cleaner than disproving by contradiction, but maybe
it's a personal preference.)
I spent at least an hour just staring at delta epsilons, and I think I can actually do them now (I've completely forgotten what I learned last semester in calculus). Looking at examples really help!
I finished my 'cheat sheet' (I just added a bunch of things onto the back of the one for test 1 since those things are still relevant), and I think I'll head to bed now.
I feel that through the large amount proofing we had to do in assignment 2, I've got a pretty solid fundamental understanding of the structuring and execution of a good proof, although delta epsilons have been haunting me since the day we introduced it in calculus, so I'll definitely be paying very close attention to those.
Some other helpful things I decided to include:
Ceiling(x): the smallest integer no smaller than x
Prove ]x[ + 1 > x:
Since ]x[ + 1 > ]x[ and we know ]x[ > x (by definition of ceiling)
Then ]x[ + 1 > ]x[ >= x
So ]x[ + 1 > x
Strategies for proofs:
1. Sometimes changing the direction and proving the contrapositive is easier.
Example: For all whole numbers x, if x^ 2 , then x is even.
Proving directly would be difficult, but proving that if x is not even, then x^2 is not even
is fairly simple to do.
2. Disprove a statement by negation (I find it simpler and cleaner than disproving by contradiction, but maybe
it's a personal preference.)
I spent at least an hour just staring at delta epsilons, and I think I can actually do them now (I've completely forgotten what I learned last semester in calculus). Looking at examples really help!
I finished my 'cheat sheet' (I just added a bunch of things onto the back of the one for test 1 since those things are still relevant), and I think I'll head to bed now.
♩ヽ(・ω・ヽ*)♬ Good luck everyone! ♪(*ノ・ω・)ノ♫
Wednesday 13 March 2013
Another update?
It's been a while since my last post hasn't it? Turns out, keeping a blog is harder than I thought it would be - since everything else I have to do has a certain deadline, this blog always seems to be the thing that gets left behind, WHICH IS WHY I have decided to set a deadline for myself: from now on until the end of the semester, I will be making a post every friday night, and if I have time, every monday night too just to make sure that I have a concrete understanding of the material.
Since I find that the material of the course is getting a little more complicated, and things such as efficiency are a little harder to understand, this seems to be a good way to ensure that I'm getting a good grasp of the material.
I. Will. Abide. By. This. I. Promise.
Since I find that the material of the course is getting a little more complicated, and things such as efficiency are a little harder to understand, this seems to be a good way to ensure that I'm getting a good grasp of the material.
I. Will. Abide. By. This. I. Promise.
Sunday 10 February 2013
Thoughts After Test 1
Wow it's been over 2 weeks since my last post... the workload really piled up over the last few weeks and that really made committing to making one post per week very difficult for me.
Since I didn't really have time to test prep material this week. I guess I'll just jot down some thoughts of the first test.
Since I have a pretty good understanding of the course material so far, I feel that the test was relatively easy and there were no surprises in terms of difficulty in any of the questions (although I did wish that I'd never have to see delta-epsilon proofs after calc).
Here are some of the things that I put on my cheat sheet that I might need for further references:
Implication:
P ⇒ S ⇔ ¬P ∨ S
Exclusive 'or':
(P ∨ S) ∧ ¬ (P ∧ Q)
P ⊕ Q (this is the notation for exclusive or!) = (P ∧ ¬ Q) ∨ (¬ P ∧ Q)
Converse/Contrapositive/Negation: Wikipedia
One more week until Reading Week!!!
(づ。◕‿‿◕。)づ
Thursday 24 January 2013
Assignment 1: Getting Started (This Week So Far) with Mathematical Notations
So far, I think I'm getting a pretty good grasp of the course material. (i.e, how to use venn diagrams to illustrate certain sets, implications, etc).
I DID find the usage of 'but' quite surprising, because I always used/interpreted 'but' with somewhat of a contradictory sense, but it is also a logically inclusive term (see? an use for 'but' as an addition to what I was saying before).
I also found the 'inclusive/exclusive or' in logic very interesting, because in real life, we use 'or' as a choice between options, and use 'and/or' for inclusive selection, but in logic it would just be 'or'. I think this is something that took a while for me to get used to in high school, when we were first introduced to notation for calculus.
ALSO in the spirit of beginning to tackle Assignment 1, I'm going to make a sufficiently comprehensive rundown of the symbols I'm gonna need to write this assignment (thanks Wikipedia):
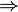 : implication, A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B.
: implication, A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B.
 : equivalence, A ⇔ B means A is true if B is true and A is false if B is false
: equivalence, A ⇔ B means A is true if B is true and A is false if B is false
 : logical negation, the statement ¬A is true if and only if A is false.
: logical negation, the statement ¬A is true if and only if A is false.
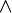 : logical conjunction, the statement A ∧ B is true if A and B are both true; else it is false.
: logical conjunction, the statement A ∧ B is true if A and B are both true; else it is false.
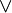 : logical disjunction, the statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is
: logical disjunction, the statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is
false.
 : universal quantification, ∀ x: P(x) means P(x) is true for all x.
: universal quantification, ∀ x: P(x) means P(x) is true for all x.
 : existential quantification, ∃ x: P(x) means there is at least one x such that P(x) is true.
: existential quantification, ∃ x: P(x) means there is at least one x such that P(x) is true.
 ,
,  : set membership, a ∈ S means a is an element of the set S;[6] a ∉ S means a is not an element of S.
: set membership, a ∈ S means a is an element of the set S;[6] a ∉ S means a is not an element of S.
 ,
,  : subset, (subset) A ⊆ B means every element of A is also an element of B.[7]
: subset, (subset) A ⊆ B means every element of A is also an element of B.[7]
(proper subset) A ⊂ B means A ⊆ B but A ≠ B.
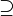 ,
, 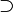 : superset, A ⊇ B means every element of B is also an element of A.
: superset, A ⊇ B means every element of B is also an element of A.
A ⊃ B means A ⊇ B but A ≠ B.
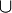 : set union, A ∪ B means the set of those elements which are either in A, or in B, or in both
: set union, A ∪ B means the set of those elements which are either in A, or in B, or in both
 : set intersection, A ∩ B means the set that contains all those elements that A and B have in common.
: set intersection, A ∩ B means the set that contains all those elements that A and B have in common.
Alright I think these are all we'll probably need for this assignment. Goodnight and good luck!
I DID find the usage of 'but' quite surprising, because I always used/interpreted 'but' with somewhat of a contradictory sense, but it is also a logically inclusive term (see? an use for 'but' as an addition to what I was saying before).
I also found the 'inclusive/exclusive or' in logic very interesting, because in real life, we use 'or' as a choice between options, and use 'and/or' for inclusive selection, but in logic it would just be 'or'. I think this is something that took a while for me to get used to in high school, when we were first introduced to notation for calculus.
ALSO in the spirit of beginning to tackle Assignment 1, I'm going to make a sufficiently comprehensive rundown of the symbols I'm gonna need to write this assignment (thanks Wikipedia):
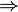 : implication, A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B.
: implication, A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. : equivalence, A ⇔ B means A is true if B is true and A is false if B is false
: equivalence, A ⇔ B means A is true if B is true and A is false if B is false : logical negation, the statement ¬A is true if and only if A is false.
: logical negation, the statement ¬A is true if and only if A is false.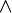 : logical conjunction, the statement A ∧ B is true if A and B are both true; else it is false.
: logical conjunction, the statement A ∧ B is true if A and B are both true; else it is false.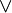 : logical disjunction, the statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is
: logical disjunction, the statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false.
 : universal quantification, ∀ x: P(x) means P(x) is true for all x.
: universal quantification, ∀ x: P(x) means P(x) is true for all x. : existential quantification, ∃ x: P(x) means there is at least one x such that P(x) is true.
: existential quantification, ∃ x: P(x) means there is at least one x such that P(x) is true. ,
,  : set membership, a ∈ S means a is an element of the set S;[6] a ∉ S means a is not an element of S.
: set membership, a ∈ S means a is an element of the set S;[6] a ∉ S means a is not an element of S. ,
,  : subset, (subset) A ⊆ B means every element of A is also an element of B.[7]
: subset, (subset) A ⊆ B means every element of A is also an element of B.[7](proper subset) A ⊂ B means A ⊆ B but A ≠ B.
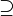 ,
, 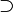 : superset, A ⊇ B means every element of B is also an element of A.
: superset, A ⊇ B means every element of B is also an element of A.A ⊃ B means A ⊇ B but A ≠ B.
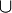 : set union, A ∪ B means the set of those elements which are either in A, or in B, or in both
: set union, A ∪ B means the set of those elements which are either in A, or in B, or in both : set intersection, A ∩ B means the set that contains all those elements that A and B have in common.
: set intersection, A ∩ B means the set that contains all those elements that A and B have in common.Alright I think these are all we'll probably need for this assignment. Goodnight and good luck!
**✿❀(。◕ˇ∀ˇ◕人)❀✿**
✿*,(*´◕ω◕`*)+✿.*
Wednesday 16 January 2013
Hello World!
Testing testing!
Okay so, I guess this is where I will be recording my progress during CSC165 this semester.
Hopefully by the end of the semester, when I look back on this thing I won't embarrass myself with how dumb I was. (But then it's all part of the learning progress, right??)
More shenanigans to come.
Okay so, I guess this is where I will be recording my progress during CSC165 this semester.
Hopefully by the end of the semester, when I look back on this thing I won't embarrass myself with how dumb I was. (But then it's all part of the learning progress, right??)
More shenanigans to come.
Subscribe to:
Posts (Atom)